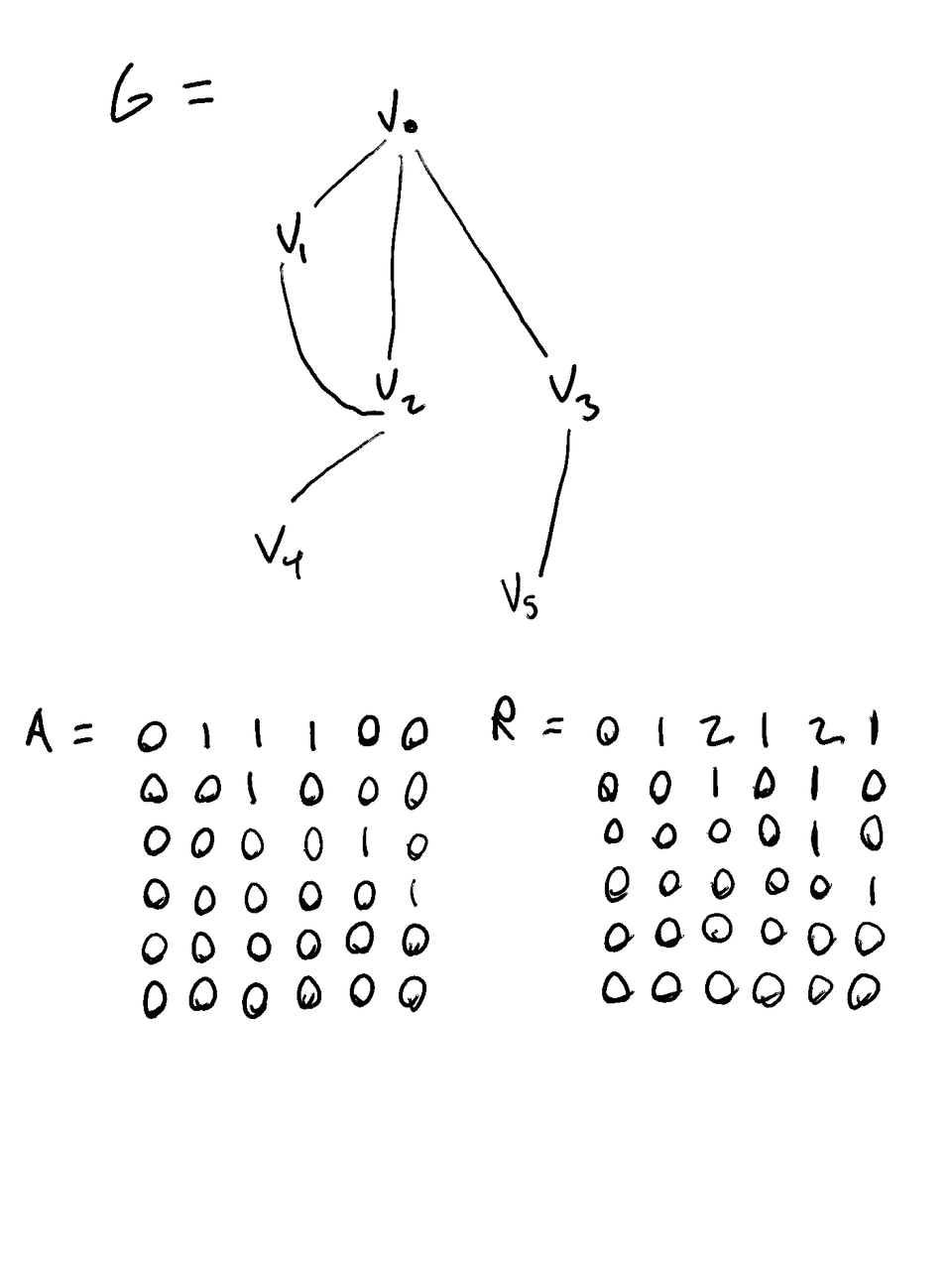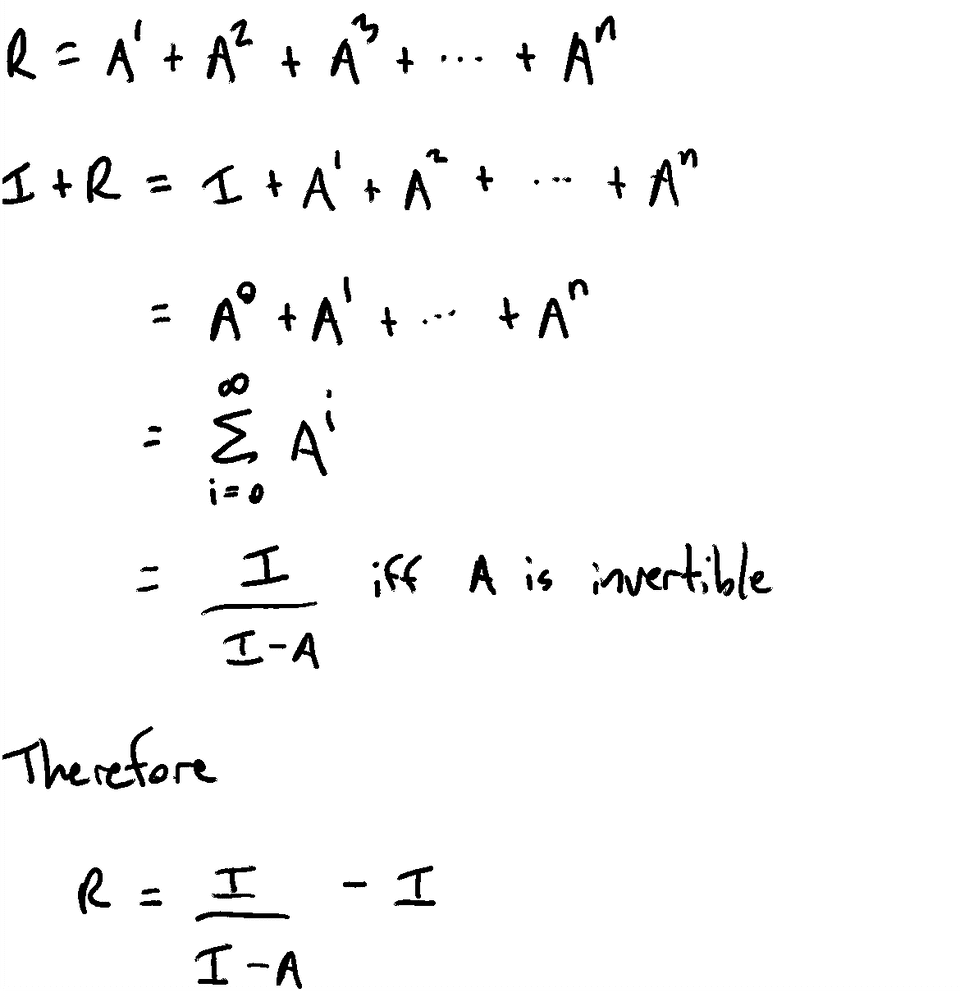We describe an algorithm for performing efficient reachability queries on DAGs using reachability matrices.

Constraints on our Graphs

The graphs supported by this algorithm have the following constraints:

• Directed
• Acyclic
• Single connected component
• Distinct edges

Definitions

• Let G be our graph

• Let A be the Adjacency matrix of G

  • Where A[i][j] == 1 iff Vi is a parent of Vj, 0 otherwise

• Let A^n be the Walkability matrix

  • Where A^n[i][j] == the number of walks of length n from Vi to Vj

• Let R be the reachability matrix

  • Where R[i][j] == the number of walks of any length from Vi to Vj

Example

Queries

getAncestors(Vertex v)

The column for a vertex encodes the information about which other vertices are ancestors.

Retrieve the column for v

For each vertex j

    If col[j] >= 1, j is an ancestor of v

getDescendants(Vertex v)

The row for a vertex encodes the information about which other vertices are descendants.

Retrieve row for v

for each vertex j

    If row[j] >= 1, j is a descendant

doesPathExist(Vertex to, Vertex from)

Return R[from][to] >= 1

Constructing the Reachability Matrix

Proof the Series Converges

The series must converge because our graph does not allow cycles. Therefore, every walk must be finite and there must be some n where A^n is the empty matrix. Therefore, the series must converge.

Mutations

addEdge(Vertex a, Vertex b)

We want to add an edge from a to b.

Update a’s ancestors

We need to update a’s ancestors to show they have paths to b and all of b’s descendants. For every descendant of b, j, there is now an additional path from every ancestor to j.

The row for b contains the entries for every vertex b can reach. We can add the row for b to the row’s for a and every ancestor of a.

For each ancestor i of b:
    row_i = row_i + row_b

Update b’s descendants

We need to update b’s descendants to show there are paths from a and all of a’s ancestors. For every ancestor of a, i, there is now an additional path from i to every descendant.

The column for a contains the entries for every vertex a can be reached from. We can add the column for a to the columns for every descendant of b.

For each descendant j of b:
    col_j = col_j + col_a

Update R[a][b]

R[a][b] = R[a][b] + 1

removeEdge(Vertex a, Vertex b)

Remove an edge from a to b.

Update a’s ancestors

We need to update a’s ancestors to remove paths to b and all of b’s descendants.

For each ancestor i of a:
    row_i = row_i - row_b

Update b’s descendants

We need to update b’s descendants to remove paths from a and all of a’s ancestors.

For each descendant  j of b:
    col_j = col_j - col_a

Update R[a][b]

R[a][b] = R[a][b] - 1

addVertex(Vertex v, List parents)

To add a vertex, we add an empty row and column to the matrix. If n is the number of vertices, R is an n x n matrix. When we add a vertex, R becomes an n+1 x n+1 matrix. Each parent must be distinct.

Add row and column
For each parent:
  addEdge(parent, v)

removeVertex(Vertex v)

To remove a vertex v, it must be a leaf. Otherwise, the graph would become disconnected.

Remove the row and column for v

Time Complexity for Adding and Removing an Edge

Dimension of our Reachability Matrix

Let n be the number of vertices, then we have an n x n reachability matrix

Remove the leaf rows

Let k be the number of leaves

• Every leaf will always have a sparse row
• Remove k - 1 rows (at most we could be affecting 1 leaf with our mutation)
• We now have an n x (n - k + 1) matrix

How many entries in our matrix can be non-zero?

Observe that if we sort our vertex columns by ascending depth in the graph

• We get an upper diagonal matrix

  • Half of our entries will be 0
• There are at most n * (n - k + 1) / 2 entries that could be populated

Adding and removing an edge is an O(n * (n - k + 1) / 2) operation where n is the number of vertices and k is the number of leaves.

Note that each operation is a scalar addition or subtraction.